Spectral Morphing in HISE

[DanH]

Digging this up in case any advancements have been made in the spectral morphing area?!!

Could Max MSP do it?

[HISEnberg]

@DanH I don't think you will make it far in Max MSP if your intention is to bring it into HISE. RNBO's fft performs poorly, and Gen~ doesn't really have a viable fft option. Max itself has some good options for spectral processing but nothing exportable to C++

[mmprod]

@HISEnberg what would you use for fft processing if RNBO is not a viable option? and I’ve also heard that Faust is not optimal for this either

[HISEnberg]

@mmprod It's on my bucket list to do a deep dive into the Loris library, which I think has the solution. I have only scratched the surface here, but it is seriously impressive what it can do. My understanding with Loris is that it can't be used for live processing (though I could very well be mistaken on this).

RNBO, unless they have updated their FFT objects, would be my go to but from experience I know it is not useable. Otherwise the task probably involves some external C++ which is not a simple feat. I wonder if @griffinboy , the GOAT for external C++ implementation has looked into it?

[griffinboy]

@HISEnberg

spectral? Haha it's on my list but I've never done it before. I'm very interested in linking up neural networks to spectral synthesis in the future but I've not got an external node for that yet : )

Most of my finished nodes are for analog modelling, filters, compressors, etc.

[clevername27]

@Christoph-Hart said in Spectral Morphing in HISE:

"Now that we've invented electricity, where are the self-driving cars"?

Are you Elon Musk?

[aaronventure]

@clevername27 It's funny how even on this forum I cannot get away from hearing about this fucker.

[clevername27]

@aaronventure Right?

"OK, I found HISE on the internet. Why isn't my plugin finished?" — Phoney Stark

[hisefilo]

@Christoph-Hart

Got stuck on this:

lorisManager.process(file, "morph", ??????????

I'm implementing dilate without issues

lorisManager.process(file, "dilate", dilatePoints);	

Is "morph" available as "dilate" and "shiftPitch" are?

Hope you can shed some light on this topic :)

[clevername27]

@hisefilo @aaronventure I'm thinking you can just use the FFT object in HISE, in real-time. Anything more than crossfading between the amplitudes may be too much, though. Use straight C or C++ for any sort of real DSP.

Take DFTs of the source and destination. Measure the amplitude (i.e., magnitude) difference between each of the buckets. Crossfade between them. There are some phase issues, but given your application, I they may not matter.

I haven't looked at HISE's object, but assuming it just takes in audio stream, and returns buckets, we're only talking about a few lines of code in HISEscript. Just ensure that you start and finish the matrices at the same time. I can go into more detail.

I have taken a look—yes, it's just a few lines a code to do what you want. Preallocate your buffers; it looks like prepare will do that. The setMagnitudeFunction call looks like it lets you define a single function to process the bins, which is helpful in your case, because ostensibly, you want to do the same thing to all of them. I'm not clear what process does. Depending on what you want to do, the windowing function doesn't matter. You may wish to play around with the weighting of the bins, as the ear responds differently to different frequencies. Again, I'm not sure what you want to achieve, perceptually, but see if you perform your tasks without worrying about phase—you need to process the bins as quickly as possible, as HISEscript is not optimal for this. Use setEnableInverseFFT to reconstruct the signal.

All that being said, I would suggest listening to examples of spectral morphing. Much of the time, it's indistinguishable from simply crossfading the summed audio signals.

Start with what you want to achieve, perceptually, and work backwards from there.

[ustk]

@clevername27 said in Spectral Morphing in HISE:

All that being said, I would suggest listening to examples of spectral morphing. Much of the time, it's indistinguishable from simply crossfading the summed audio signals.

That's what I was thinking, if you crossfade between to FFTs, that'll be the same as crossfading gains in time domain.

Also, let say you do not apply the same weight to different bins. Wouldn't this be equivalent to filtering both signals before applying a crossfade in the time domain?

There are some phase issues...

Yeah I've seen this here and there when starting to play with magnitude ins... But in that case, wouldn't crossfading the phase bins at the same time as magnitude ones prevent any issues?

[clevername27]

@ustk said in Spectral Morphing in HISE:

That's what I was thinking, if you crossfade between to FFTs, that'll be the same as crossfading gains in time domain.

While perceptually, there may be little difference, I wouldn't quite characterise it as being the same. I'm still a little unclear about "spectral morphing", as I'm not aware of it as a formal term. In as much as I can surmise your purpose, one way to think of the distinction is that cross-fading amplitudes occurs in the time domain, while cross-fading FFT bins could be characterised as occurring the frequency domain.

Also, let say you do not apply the same weight to different bins. Wouldn't this be equivalent to filtering both signals before applying a crossfade in the time domain?

I would suggest applying different weighting, as auditory processing is not strictly linear in terms of frequency response.

Yeah I've seen this here and there when starting to play with magnitude ins... But in that case, wouldn't crossfading the phase bins at the same time as magnitude ones prevent any issues?

It's a good question, but I want to avoid wading into the phase issues of DFT as they are non-trivial. I would suggest starting with a simple interpolation of magnitudes between frequency bins.

[hisefilo]

@clevername27 hello professor! sorry for the delay. And for my lack of preparation!
I want to achieve this kind of morph https://www.cerlsoundgroup.org/Kelly/sounds/trumpetcry.wav

I actually want to start trying to use amplitudes from one audio with freqs from the other one to see what happens.
I can see Loris already prepares freqs and amps for morphing when I do

lorisManager.createEnvelopePaths(file, "frequency", 1);

Interface: distilling 24314 Partials
Interface: sifting 24314 Partials
Interface: collating 24330 Partials
Interface: distilling 24266 Partials
Interface: sifting 24266 Partials
Interface: collating 24276 Partials
Interface: channelizing 24330 Partials
Interface: channelizing 24276 Partials
Interface: Prepare partial list for morphing

And this is how it's made on C++ but can replicate on HISE.
Going the FFT way is much harder for my level I guess.

#include "loris.h"

#include <stdio.h>
#include <stdlib.h>
#include <strings.h>

int main( void )
{
   #define BUFSZ (3*44100)
   double samples[ BUFSZ ]; /* clarinet is about 3 seconds */
   unsigned int N = 0;
   
   PartialList * clar = createPartialList();
   PartialList * flut = createPartialList();
   LinearEnvelope * reference = 0;
   LinearEnvelope * pitchenv = createLinearEnvelope();

   LinearEnvelope * morphenv = createLinearEnvelope();
   PartialList * mrph = createPartialList();   

   double flute_times[] = {0.4, 1.};
   double clar_times[] = {0.2, 1.};
   double tgt_times[] = {0.3, 1.2};
   
   
   /* import the raw clarinet partials */
   printf( "importing clarinet partials\n" );
   importSdif( "clarinet.sdif", clar );
      
   /* channelize and distill */
   printf( "distilling\n" );
   reference = createF0Estimate( clar, 350, 450, 0.01 );
   channelize( clar, reference, 1 );
   distill( clar );
   destroyLinearEnvelope( reference );
   reference = 0;
      
   /* shift pitch of clarinet partials */
   printf( "shifting pitch of clarinet partials down by 600 cents\n" );
   linearEnvelope_insertBreakpoint( pitchenv, 0, -600 );
   shiftPitch( clar, pitchenv );
   destroyLinearEnvelope( pitchenv );
   pitchenv = 0;
   
   /* import the raw flute partials */
   printf( "importing flute partials\n" );
   importSdif( "flute.sdif", flut );
   
   /* channelize and distill */
   printf( "distilling\n" );
   reference = createF0Estimate( flut, 250, 320, 0.01 );
   channelize( flut, reference, 1 );
   distill( flut );
   destroyLinearEnvelope( reference );
   reference = 0;

   /* align onsets */
   printf( "dilating sounds to align onsets\n" );
   dilate( clar, clar_times, tgt_times, 2 );
   dilate( flut, flute_times, tgt_times, 2 );
   
   /* perform morph */
   printf( "morphing clarinet with flute\n" );
   linearEnvelope_insertBreakpoint( morphenv, 0.6, 0 );
   linearEnvelope_insertBreakpoint( morphenv, 2, 1 );
   morph( clar, flut, morphenv, morphenv, morphenv, mrph );
   
   /* synthesize and export samples */
   printf( "synthesizing %lu morphed partials\n", 
           partialList_size( mrph ) );
   N = synthesize( mrph, samples, BUFSZ, 44100 );
   exportAiff( "morph.aiff", samples, N, 44100, 16 );
   
   /* cleanup */
   destroyPartialList( mrph );
   destroyPartialList( clar );
   destroyPartialList( flut );
   destroyLinearEnvelope( morphenv );
   
   printf( "Done, bye.\n\n" );
   return 0;
}

[clevername27]

@hisefilo Sure, I will try to help you out here. Off the bat, I'm not too familiar with Loris, other it sounds like a Dr. a Doctor Seuss character. Looking at your code, it looks a lot like C, and that's a good thing.

A Choice of Language

Loris is a C++ library, but you can access using C, and I suggest you do this.

The thing about C is that everything you see usually has one meaning, and that meaning is not contextual. In contrast, there's C++, where the same snippet of code can do 100 different things. So C++ is great to program in, and terrible if you're trying to understand what some other developer has wrought. (Although not as bad as LISP, a language entirely designed for computer science students to write recursive decent parsers with.)

The other thing about C++ is what I call Bill's Law: C++ is sufficiently that no one person knows everything it does. The inverse is also true: it's possible to write C++ that is remarkably clear in its form and function. But if you're a C++ programmer who does this, then sadly, you don't exist.

So why does C code (generally) only do one thing? To make writing a C compiler easier. Specifically, so it can be easily translated to assembler language. Back when C was designed, processors were slow, and memory was capricious; so if you wanted things to run quickly (i.e., be compiled) you needed to do it quickly and efficiently. (Everybody has a great idea for a computer language until they need to write the compiler for it.)

OK, so why is this relevant for morphing sound? Because even if you're brand new to procedural programming, because writing C, and understanding C, are easier than working in C++. And because I’m trying to hide the fact that I know little about Loris, so I’m talking about things I might know.

A First Look at the Code

So, let's take a look at this code. I’m a little unclear how it morphs sound. For starters, I don’t see anything about the window size or window function. I’m looking for something like:

analyzer_configure( resolution, width );

Wait, What Exactly is Morphing?

But let’s take a step back. How does morphing work?

One way to represent sound is as many, many sine waves. Depending on how loud each one of them is (and how that volume changes over time), you get either a piano or the sound of Bill Evans cursing because he can't get his code to compile.

So, you can:

1. Decompose a sound into a set of partials.
2. Then, a miracle occurs.
3. Put the altered partials back together.

In Loris terminology, they call this additive synthesis. But I think that’s being charitable—to me, additive synthesis means literally using sine waves. And if the folks at Loris have figured out how to decompose sounds into perfect sine waves, then they folks working on quantum mechanics will want to have a word with them.

In your code example, partials look to be contextualised FFT bins. In that case, each partial actually represents many, many partials. Usually. Because the interesting thing about a flute is that you can represent it with a small number of partials. And that's why computer science students hate flutes…because by the end of their degree, they've re-synthesised them a hundred times.

Clarinets, on the other hand, are pure evil. (Have you ever met someone who plays them?)

Representing Sound as FFT Partials

So, the first thing we want to do, if we’re morphing sound, is to specify how we’re going to represent it. FFTs (or DFTs, to be technical about it) are a remarkably imprecise way to describe sound. The advantage is that you get a lot of information about amplitude and frequency.

One of the downsides is that the more precision you get with one (frequency or time), the less you get with the other. Plus, each FFT bucket has a splash zone (“smearing”) that leaks into the other buckets. Honestly. it’s amazing you can put it all back together and get the exact same sound.

So that will morph sound. But the results probably won’t sound very good.

Loris to the Rescue

And that’s where Loris shines, because its algorithms are constructed and tuned specifically for sound morphing. So, instead of using (say) a Blackman Harris windowing function, they use Kaiser–Bessel. What is a windowing function? In Loris, you don’t need to know (since there’s only one), so we don’t need to cover that.

Loris also determines many of the necessary parameters automatically, such as dealing with uneven frequency representation across the spectrum.

That still leaves a bunch of parameters you do need to specify, and some are specifically related to getting pleasant-sounding morphs.

The most important (arguably) specifies how our sounds will be represented. In Loris, they call this the Analysis parameters. But everyone else calls them the FFT parameters.

Frequency Resolution

Let’s look at the first parameter: Frequency Resolution. Imagine chopping up a sound into equally-sized chunks of sound.

To do that, let’s take a Kaiser windowed FFT of a flute. We’ll use SpectraLayers, because I get a royalty check. Above, we see a familiar representation using only amplitude information. Below, is a DFT-derived representation.

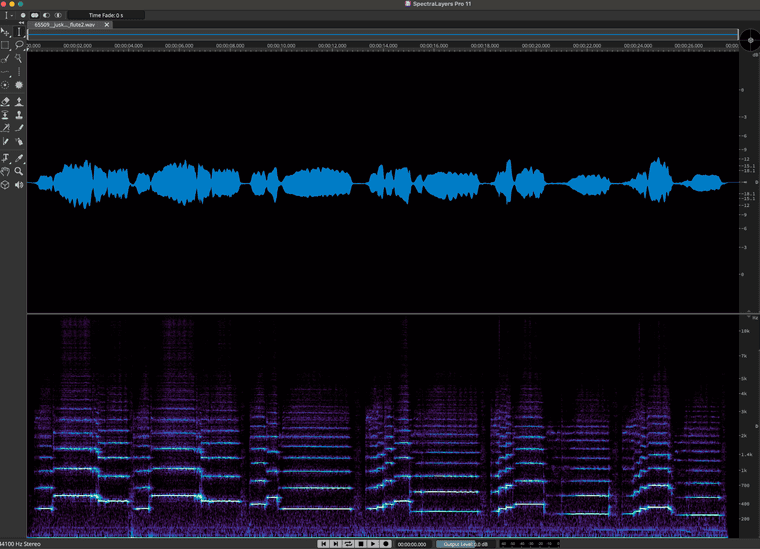
Each of those bars represents a partial. A partial represents a single sine wave. In most DFT-derived visualisations, each of these lines actually represents many partials. But with flutes, it's much closer to a 1-to-1 representation. (An additional reason for the clarity of the FFT is that SpectraLayer's creator, Robin Lobel, is very clever. He's using several high-speed optimisation techniques.)

Let's enlarge the FFT.

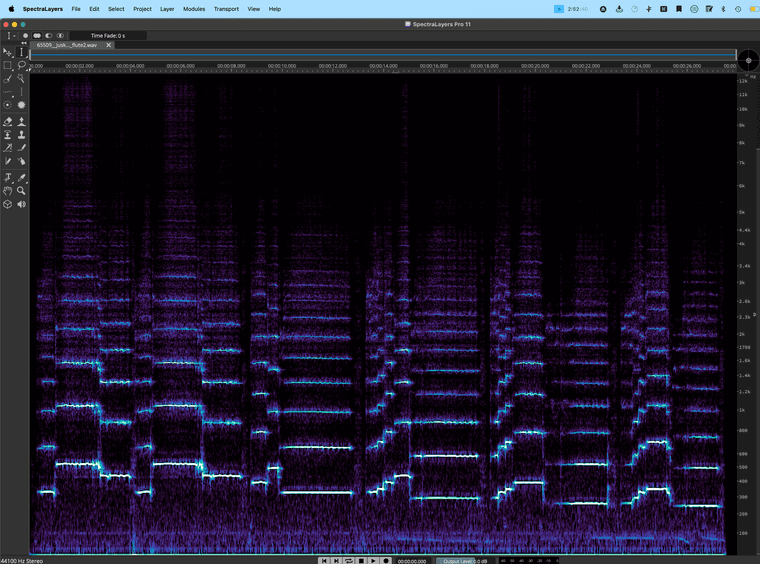
On the rights, you can see what frequencies are represented by the partials on the left. Amplitude is represented by colour, with white being the loudest. And time goes from left to right.

Now, let's look at that in 3D, so the height of a partial represents its amplitude.

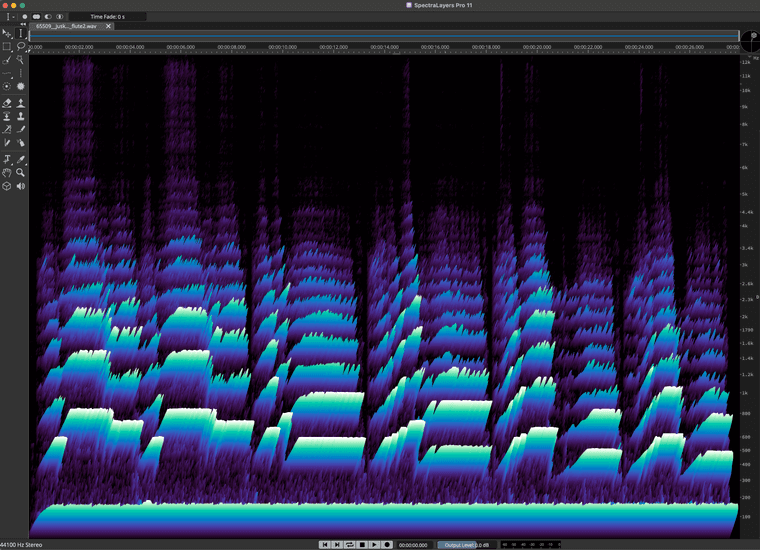
Let's restrict the colour spectrum of our flute to green:

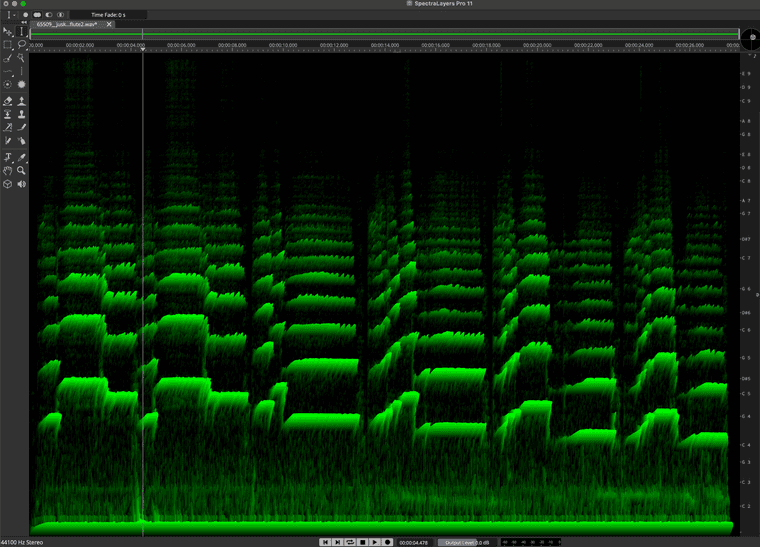
Let's look at a shorter time span of this recording:

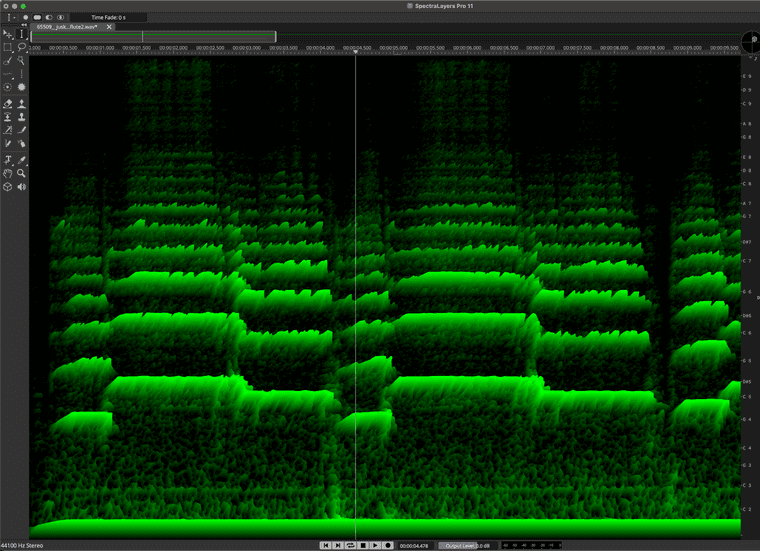
Now let's look at a clarinet and use orange to represent it:

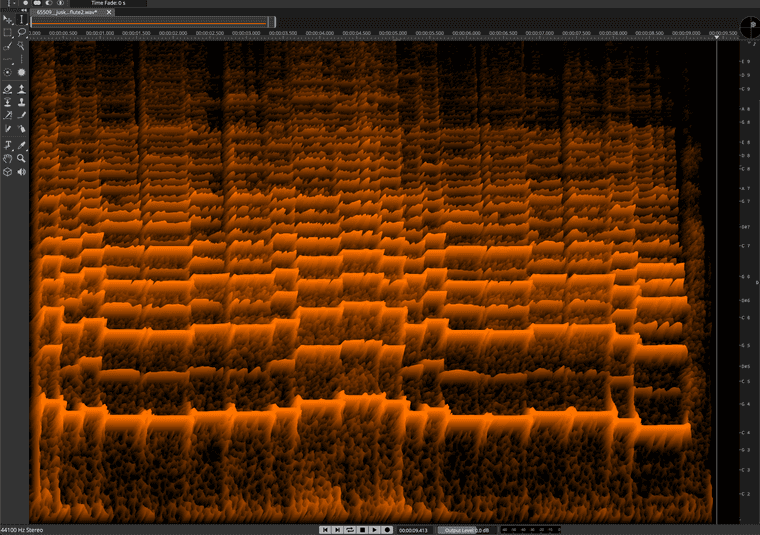
Notice the clarinet is comprised of many more partials.

Now, I'll make a quick demonstration of a crossfade between the two. With audio!

That doesn't sound cool. All of the partials are changing volume at the same rate. Boo!

Changing the FFT Bin Size

Wait, what's a bin? When we deconstruct a sound using an FFT, you end up with a grid of sounds. In Loris terminology, they're partials. Which are definitely not. We'll call them Bins.

Depending on the dimensions of the bins, we get either more frequency resolution, or more amplitude resolution. Or, to put it another way, the number of bins that you use, for dividing up the spectrum, designates the frequency resolution.

---

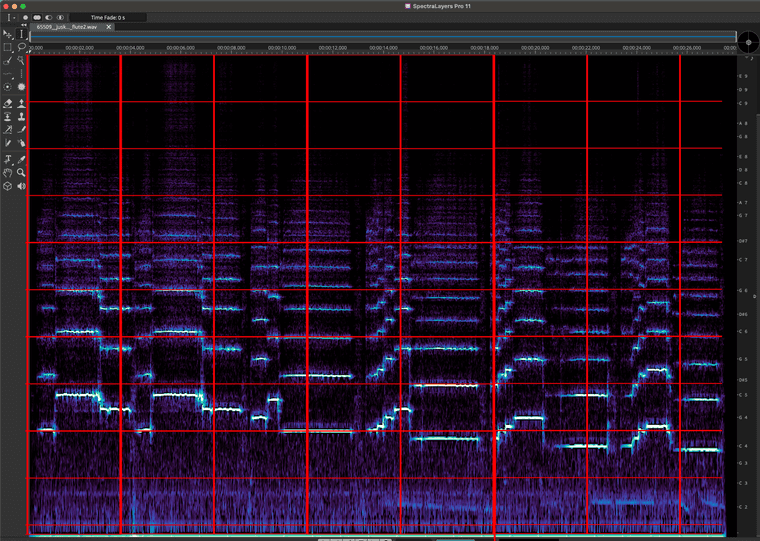
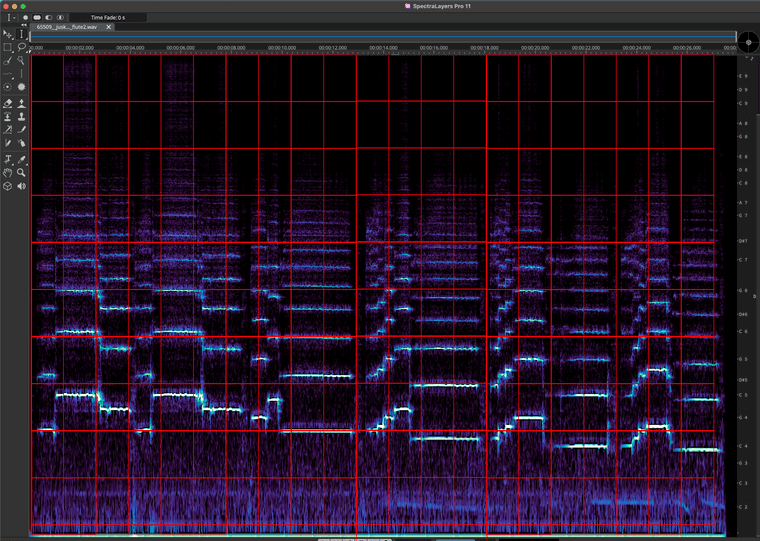
Let's change that in real-time:

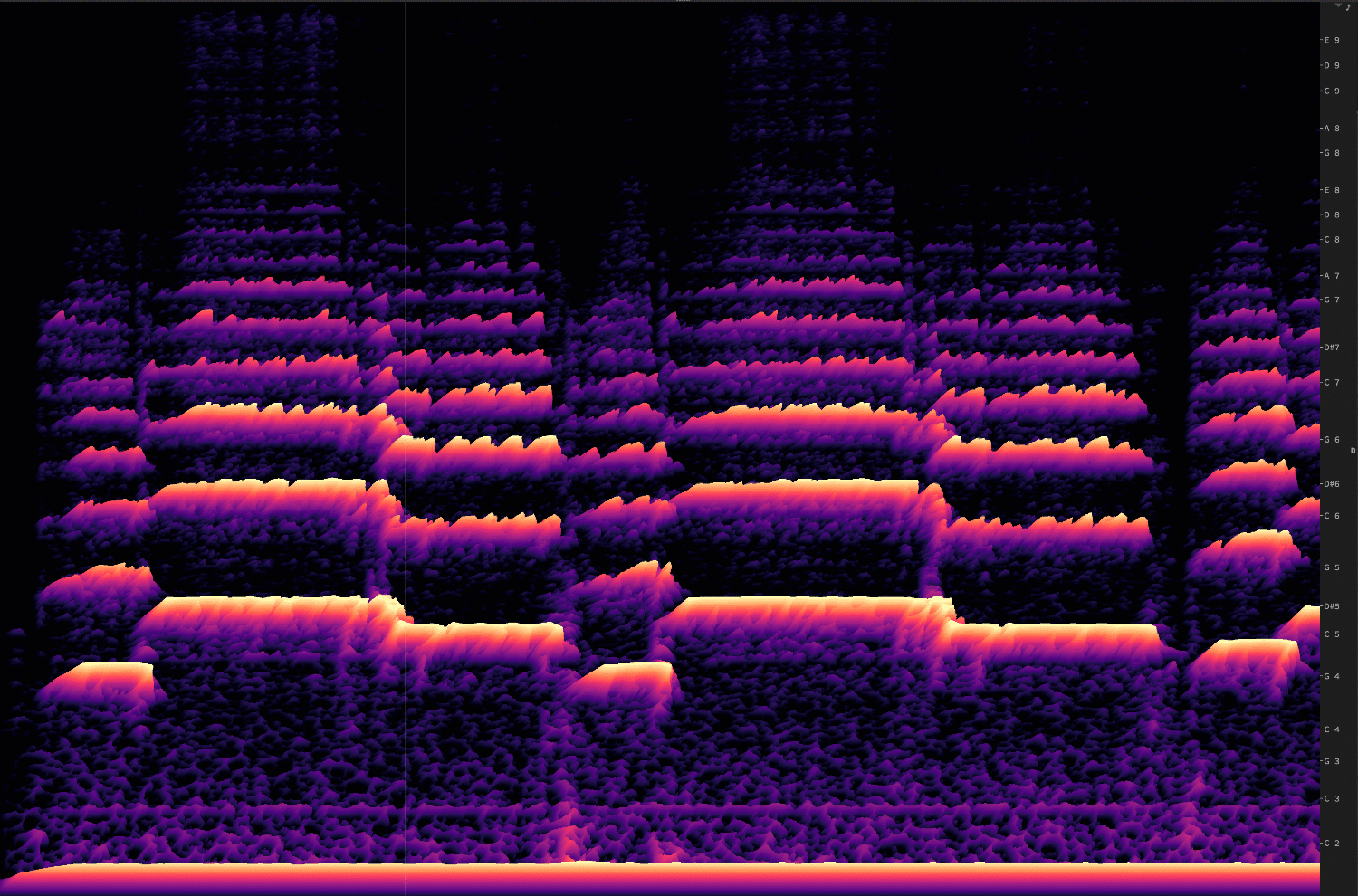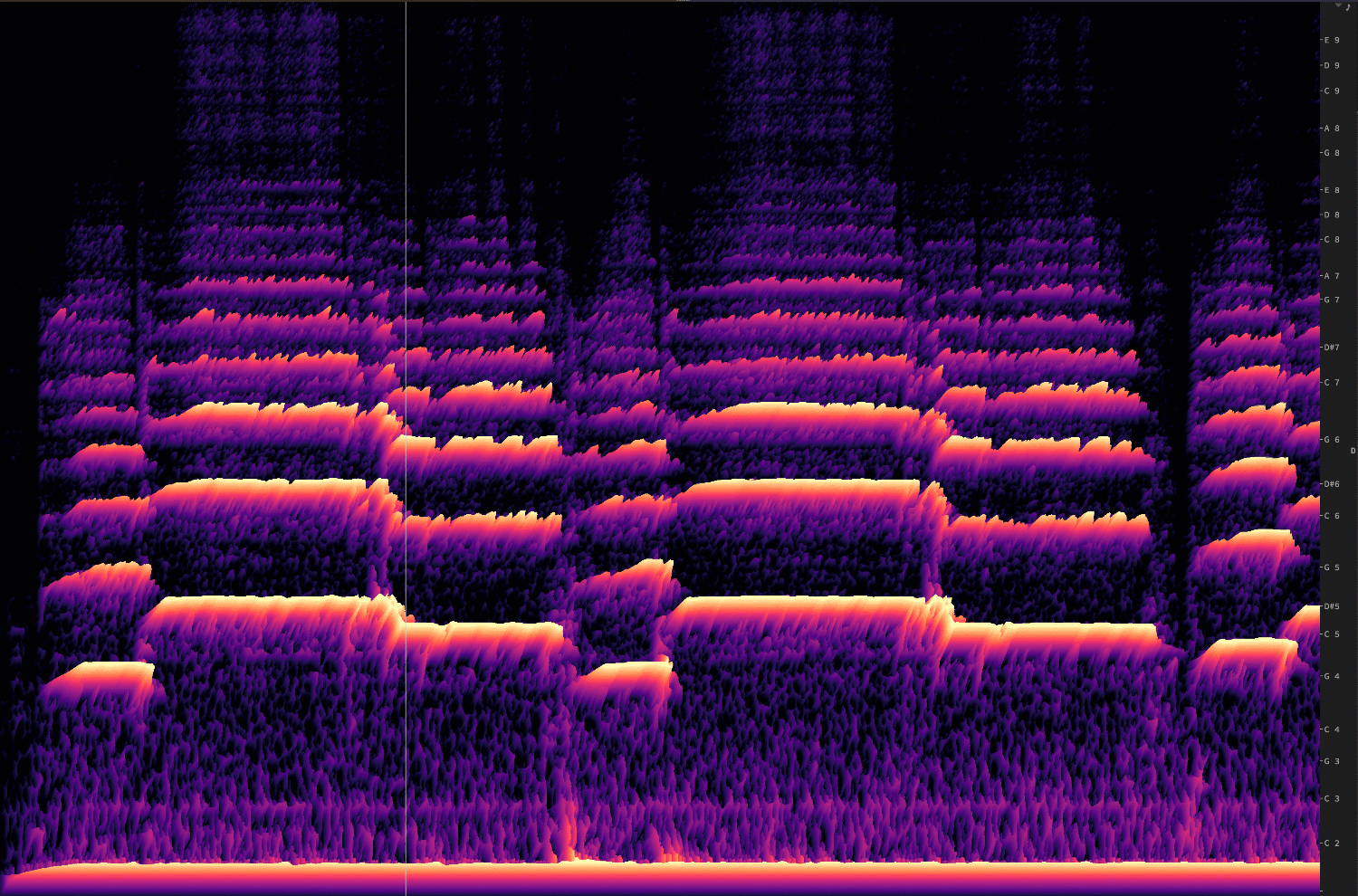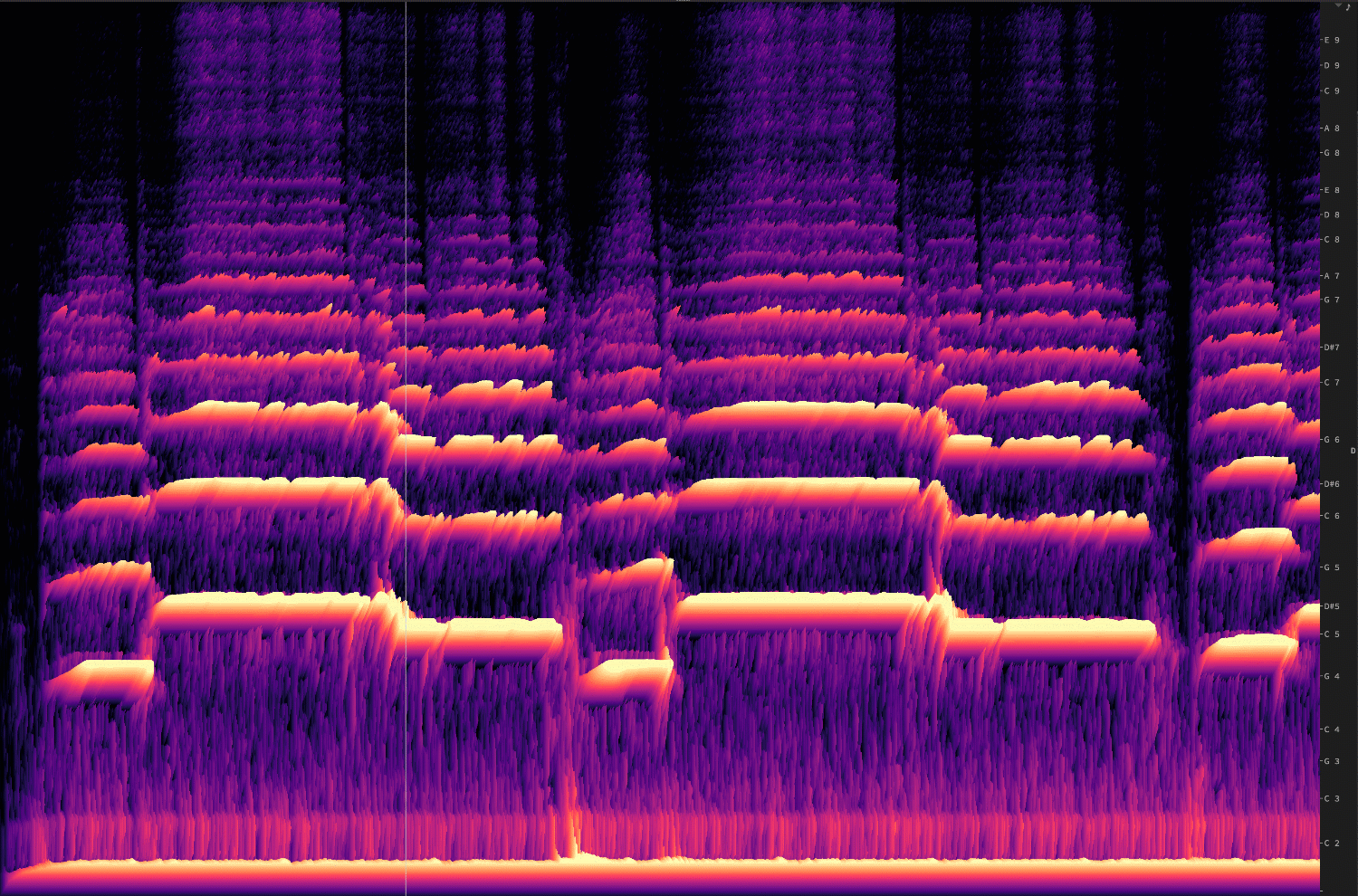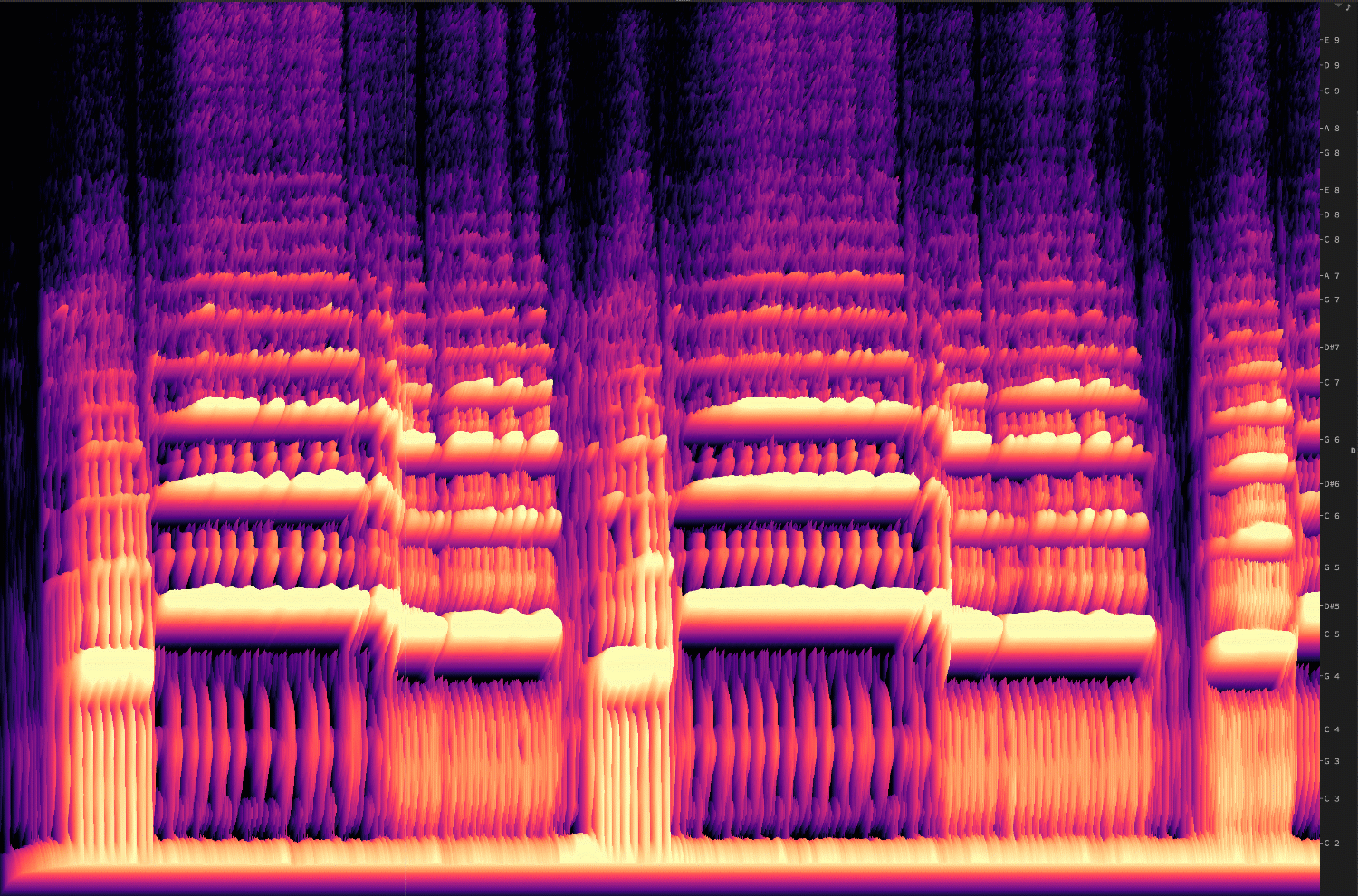
You can see how—as the frequency resolution goes down, the time resolution goes up.

Back to Loris

Now we know something about FFT analysis parameters. And that takes us back to:

analyzer_configure( resolution, width );

I'm going to stop here for now.

[Chazrox]

@clevername27

other it sounds like a Dr. a Doctor Seuss character.

lol

[griffinboy]

@clevername27

Loris is additive. And it is possible to decompose sounds into sines. I did a crude job over the weekend. You use multiresolution FFT and then try and work out where the transients would have been using FFT reassignment. And then you increase the contrast of the spectrogram and track partials pitch, phase and amplitude over time, storing them in an array. You can then manipulate the partials in this array, and reconstruct the signal afterwards. The special thing that Loris does is that it can also analyse the noise components in a signal, which is beyond what my program can do.

I'm tempted to give in and just use Loris...

[clevername27]

@griffinboy That sounds really cool, and I'd to follow your progress. Regarding sine waves—we may be taking about two different things here. Deconstructing sound into perfect sine waves, is not something that I believe is possible with our current understandings of physics and mathematics. You can certainly decompose sound into things that act like sine waves, though. I like that Loris has so many optimisations built right into it.

[hisefilo]

@griffinboy have you done that on HISE? or python Loris?

[griffinboy]

@clevername27

Maybe I'll post about it.
Ah yes - you are correct. You can't simply break a sound into it's actual sine waves perfectly (although reading some of the latest research on fft, there are some algorithms that are so good at it that it almost doesn't matter, not that I've implemented those yet). It's more a case of applying multiple passes of different FFT techniques to construct a map of everything, and then try and rebuilt something close. But unless you do a ton of passes and maybe use the most complicated fft research, there will be information lost and resolution issues

[griffinboy]

@hisefilo

Yeah it's c++ hise.

I mean, we have loris which is kind of better from the looks of it. Unless I decide to implement the latest research mine will not be better. But I can't say I care about additive to that extent. Maybe in the future I'll have a better reason to do all that work