event.drag has a "dead zone"

orange

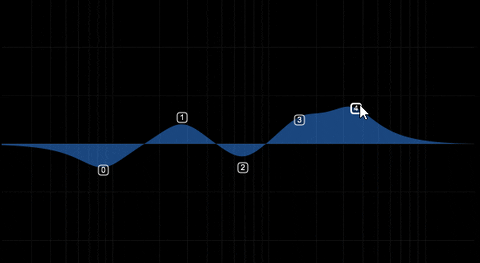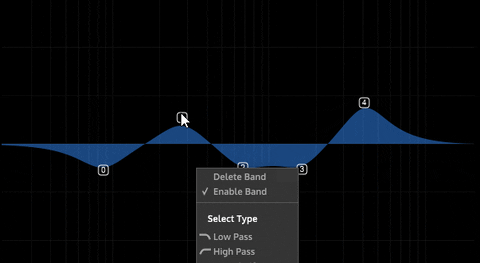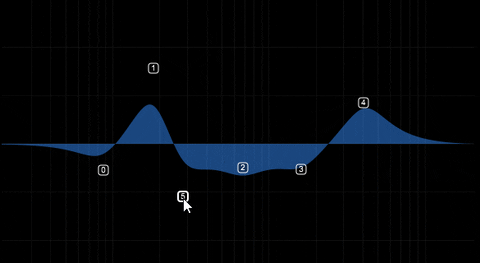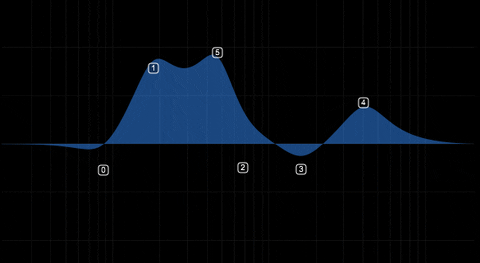
@ustk Very cool looking eq curve. This is a cool way but I think it's time to use GUI functions of the parametric eq unit in HISE GUI editor. @Christoph-Hart ? HISE need this

ustk

That's right it would be very cool

I am thinking to another use of moving the panels, so it would be cool to have the option to remove this threshold

ustk

@Christoph-Hart I'm coming back on this "issue"
The dead zone of 5 pixels when dragging into a panel is still annoying because you cannot make small adjustments, for instance, with a vector knob.
The value doesn't change, then jumps once you've reached 5px in X or Y.
This dead zone stays active when you come back on this 5px square without releasing the click and add 5 more px the other way. This creates a 10px "glitch like" behaviour where you have no possibility to come back at the starting value.

I know this allows to differentiate a click from drag, but it is so annoying with knobs, and even more with graph EQ like above...

Fortune

New Draggable Filter Panel floating looks very good and usable, thanks @Christoph-Hart

Can we disable adding new nodes by the user or limit the number of the nodes?
Can we link each node to a panel (I will make panels that contains Q, gain, type, freqq knobs for each nodes) So when the user click the node, it will make dedicated panel visible. I thought that because we can't adjust q value from this floating tile.

alt text

A Former User

I made this but the node does not matched unfortunately; @ustk @Christoph-Hart @d-healey @orange @ulrik

HiseSnippet 2106.3oc2Y80baabDGTRvIhoxw4OSlN8oKZZ6.FIQQPKm3F2NFVThNZhjEqnrbx3wiGHfij2HPbv.fxh0QS6L8k1OB4M+RmoeE5S0eG5W.2uA449hyt2Q.bfBRlR0VMS4HSIr2t29a+ys6dvsB4NznHdnVoY2cX.UqzOSu8P+3dM5Yy701XMsRk0269OdKZLMTa0gA1QQTWsRkl9t35klcFMwme31qZ6Y66PyHoosGm4P2j0mEmQsk0Wy77ZZ6R2k0Wg6Ur1vg62f6wG.XYZ8ZZA1NGX2kdOajsoz0Jck0cYw7v1w1wzHsRyrJ2cX6d7m5K4eOVDaeOJ9foVaXijjax8bQDiT0Zzi441JwlizzJo2JyCLszC7w5awbYozy7DWSr.ISBU+QooNK3YpBuZSN7Jo.uYjv6Cza6DxBhyVAw16ougODh5XCg.UXI4Uap+yUzavAN7iq129.ZyP3gTILtYsZKRV4F0pbq4JOWYHPDESNzNjf1KJVH2yiFZR9cDQxQ0tz3s3tC7rAC1XdgWQgs4ws4z1j5S1lTerM4a91V1ts78.oSrCP9F79Abe3Ai4SXX9wsgV1gPJTbH6Iq+6yYAq2oC0AjLGCmP7C746GAh8vGIVnCOjXvfmqcKBi7aI0gesvBUlq7ylqLA9HX+grGcp37qAFleAC1BlUPUoJS0HjSgGngsm29vA.CgYU4VkOFU9xKCVCyOlDxGDy7oyUNwpQQEKsibEiNC7chYbeitUFgL42cq1AN+cGOOiZGYBgc7SBNN42ckPBOTZH+UT0tgzgEIA5rNBL6srA2anseWpgzvp8HzErms2.pQExxj5nNIeFItGKBW4AL23dFUVj.4fiQaIyTvga+PX6S33qnrt8hgMboSpQySnQE0kH3hDSEElPMQci6wV2yiEDQMd3QKRFJE0r1iv.iLgABMawGDQIMVMWPQPLMZlFUnGBICUJ+LgFXcHRBUc7XNGPcIe22QjDbCs6VQvzyxvk.yt1w1UGyeKk4HvhKx2ZpZaY6wvh1igJ6QlCaIyw1kr+JMTGk33Eg4OSAqpBlFmTXeI3eJ7OrxIE.1emdHLcMJb2xVTr1w3WIQHluGbvfjDBjUTLbRNYtHjgA3.OIOxr73N1dDlK5jEZnJy2kdz1cxDJ+4.LN9o.+PJ2xMCoOQ0OMatpLnYemX3g8GDSMxuDJIgr.AyYyuxp19ta2oCHaBXklI0Cx6VdYribhJmXsgBM4ZSt8o42gz.rlC5tO9VoNVt+83wzs8Mv76YKebYx3K0oSgqkU8uvkwAFBOKAM7GzeeZXBbSXD5blu0r9o2ZVcxAGY8aEF49a3yh2Nf5eZMr0FUzGZcO0HTArFKZbe0QMta6wbggoXP+42QGaGXpI.b5vP8dgk1DKb8Lg+x+9eF9YdKs6uwZvIHb7gQvAfX.MLlgVeo0nGBykIGlXV80nQGDyC.mTZSJXZh3QSBIUZSOtMzUo6tLvKgp980UIYpcD3TKgPeXxe7TrvS13c+UqdhpHoTd4.qQXSBjOQeMnTWWaHNzj4Aykzx1m5ose2jQBkaKKl1Oixqd0q9iYTpOhoqKL9R2TWTxb9zvyFty+kjw51unfkMvy0vhKYNW4iwXXpinrzQLWxLWBPgdfx5ImBPiOal2gpOLANAny.+oI8GfnyuPuA1CHZQxWwOjFR90DgeA7zZA7fAAa6uCtEBlv46xbPydEvcH11X5QwmjppY8Nu1LREiZMqLi5EGZEESCZy9CT0g+6amw+e4eY0W8pAqXcdzbcEM+x9mOMCpJuleg1IGeFFhOYnS0I6w5fiV.pojaDZbLY+HV7PU89VYb+IEtefdKVrSuhw6TEfWrbzaY7N5xSyoKGqNCryn27atn2Tp3KxU60cSoxIE2ZLH7P55OQfi2WO2Q+bP5dC5Kq5fcGJgEQvte0F4.svhpHAS0RzHg54uAru60GmvJYDtlUyl6ttOVhS5GlNueX5IyOTPXPNzeWXJtPFVJFLm1voeGJDE7gJVBqZJrDf74ZIkSaSEVonR5qFsnYhK.WzLYQ0P8Ukt22SuMLPk35TBG7mHdl7.6Coj6R8ogXRq4o8RCd92+8+iI8kFDLwuzfschA0uKLJaT.ORsRw+rMsOaWnJTjp1teDEm2ZG7TjJ8Fb6vBW5GtcSvHKTl11wCBEGGuSe9.+3bG+l9+xb9Be6.y7S5WdwkWw2omL3VfGbpVm3EfcMHMtefGcc+CodvXSBL9gvbRcrG3EmPMed8VbedPOtOyQMnuCVqoaWZnJ1Kzffoysw94IT9XqcndTa0D3eo0lPhmcH3mnWPewYWEon20TgwqettDtD7vH4mTMMGUYRWeylaOJ2B9KRpQX95v3KuMdzd.02Iin0JVXomMTlrfYgU45vC6OpSSZI9MocAEoZz6Rggefpj4RMZ2mygq5hyOmVP6428e+QVax4Ao8Hx1jV8fjA4swxUlZPTLueBVDulz1vPRxAfen9muRU3SmEvu+MMfut91uYdV6MWV2TSXV2GIhjogLLldYVnnfwKjUTytz5nBEi+1Pe8nDZBsqs.FpkIfo+iUSBzzx1z6Itna5Z+oGXISnx2djYMpn0dpWu7ucimZksSBEKyW9U50E4KJeNbr3+S19MWjW6bE3SOV9+x.+rmm.e8KRfWS6sVf+4Ge0O05RO5clWUY5+O5pJmCnbYLt9kgN5a6DxeriL4DOq7tBJfc6K9OsaV8svmIoueKc8ZUqo0GNm7XGGzcuD3eJVl5W.Yt9EPlUt.xbiKfLe9EPlu3BHyMOSYvRT2Y.Lxf7nHPn05xh+kTtXp1OhORhfx

ustk

@Steve-Mohican Because the value you handle shouldn't be linear but logarithmic.

ustk

@Steve-Mohican I've made my own GraphEQ a few months ago before @Christoph-Hart made the curve EQ accessible.
If I knew at that time I wouldn't go through all this pain But I learned so much!

ezgif.com-video-to-gif-2.gif

ulrik

@ustk that's really good looking!

ustk

@ulrik Thanks ;)

orange

@Steve-Mohican

Yeah you can use logaritmic or other non-linear equations for this kind of implementations. Here is my method, I used a "Hyperbolic Decline Equation" method for the frequency cordinates.

Cheers ;)

HiseSnippet 2270.3oc2Y07aabbEeojWaK5p7QgKPPALvTghhkVjT6tjTTr1ElRhTQBIxhUT0IAFFFq1cH4.sbG58CIw3XfbL8TOzK9OGeonG5k.zS8T8eAE9dOn7lY3xcVJZIFAXijPCKw48wLu2u27dyaF0xmZiCBn9JYV3fgCvJY9UpsG5E1aydVDOkcZ.zUa9rm5QcvJaLbfUP.1QISl4+TF6LKbME9m27fMrbs7rwIjTTdDkXi+bReRXB0V0+Lhq6VVN3CH8kjtb8crodaRcoQfoLuptx.K6ir5henESr4TUxb8lNjPpe6PqPbfRlqsA0YX6dzS7Dx+HR.4PWLafgRaXhDj2h55vrX12U1rGw0oUrKGnnjQsUB.Lu..ts5tDGxX5I.wGwYfRzPFOxL2EYdFxlm9TMOioYdYjLuqILuOVsssOYPXBGlscK0c7Bw9crrSGlDxpLWoaptIEjvKrXeqiva4CCFqgV0pUyiJWQO28VLK6ePnHHDcrkO5K+pVVNs7bQ+ITr9cwgaR6Of5ACzVJVfkD5lnYKKeHzE5SdVy+rAnNeWES4lc5fsAMSIvRwKs7TbjG8v.P0G+DNyNTejFAFqeODAcejI7qkWN2hYe9hYQvGt3Ol7j2ps9Yf.KsrFYYibrkSVmhALI8B8otaZ45dHr4Si6ZLAeAa0WYEvkHdgHeZTHwCuX1XWmoKm09BNZch7rCITOst4FYZhe1sXGXy+5ttZ5mZrlN+Srgb9e1UXSrLBMwuBJND65ROYZ5vvqSAOeWK.k8s75h0D9l9SXnvirbivZ4PqfLYqJ5tnvdj.Fmuf3D1SKWdjd9IoUvXr4wl9gvzGKw1XR2dgvDV37qnw4VQokKVw7HiJ4OG03kaRLqoqKYP.V6wmlGMTnpQkmviMhMNPzYWZT.Fs4FoCLbpiCoiiL3igcDIacHcPBREscI1GgcPey2fDDb7s5lSH0ySLNtg6XEZUbBPWnzofaOM.1P1ASligSaNFJMGInVAiIlkjuMNdGDi97X8ckrUYEGGrjDu.7eI4Gl67J.yucOlY5nM0YaRluPXjihSDOWHCAEGGD0WzriyQyCaz.KgEXF4XtTaKWDwgAy70nHwyAe5dcRTJU5PR772AJkiM.1arkO9YvV0sgJn9GRgPLpA1laI6hC6QcXlFR5SpZSL.Z8PXvgQgXszr3SLZYDaKdZNaX44rWmNft4QZZFEWqrgwpqV0vnZIS8ZMWV2HGnCOpOfdBHALKZZELJZVt1ZUqXTS2zTeUilEzKk6tBTYEsBlEqtZMiJ0JWsrdYSSCXdJkC1V.JtxaQY1m6MoChhIfcgjlUVgcbN.PMnA3B6iC.fE9x1Pl2X.J0dsYFe3y6LfOLOa0J0VynrQES8RUqTVfPLLoVwRlUqVtlwZF50JUhgcl4t6XjiiMPRQQ8xqUoZESypvrTasbrROZikpTQFjTAlefcMiUYSxTTBVvKehm.PSP1wEd7wCXGHnMYhp3DtWL9rN9wZw4BTuGRCw64okK6yytP1WjEMIqNclJuQGb4h8mJaVmV9WjhZdQ8OD6Gm7EKHzxQ5dZTe68zH2xks3vWIAod63QB2a.16s0oixnSrgddlajUAhFx634CF0wSaWhC1Wg.M1bCU1Y4FJbCdbWj+y+QckYVYyTJ+sstgZck+xNMfxdr9tFYNfIBULBILuOSC7wPCshtvVPsAN3nP5.triJDAsgIVzEi6QyxC6xWyawa+B1S.1voRMIWenbGymvNpXLgO46p2iW2eLku+qqGhOMLtM4Et9YmcFmAID2WP0jQ992+95oIKS8PpO.E6a4PhBjWcA81juNUW7YTk7uECG0hrv+1xkZAc7z8.BrKf4lenpLISYW8MOHkqNBfEnInFwEZFsAIXfq0PkC6lX0kJUZ0y6KK7nyNdJN9baeVWFYdXLyZp7SrWZ7FscbV5Ohlnwy7bQ1gcnBvrfAjdNQbP+bwg2DUOYgKwVXnFLmy.Kevqj2QHE3Ujn+A+nPxRyNRtdjCgttmk6v.XIm.Iaddj7ku7k2YJHY2tcuSBRVZ5HY7xLIJZdkAwytTPLcBv+5UmcmQnvkmDlUMt.sLbp8pKHGT4uNoY+5n5Vrlvi6oDRg9spax5ZLHOZa5wXeze.0.ZZrKD6TFPGDMXOu8YSAWHQIxjvRVUiUgqeYZTIkmIQdl2RciKsbYhW25D4JOmTuuUBuu6eWuu7k6KWelMgqeoEcSVlAeqjITOsInz3RVyyeuX314TmHWqvzWYm0.xHFvYdotaL69udAjvgxoVuStG+rZterZKRncuoauyME6kcb46X6czqhrnp3d6IF60T25KupOAxOhWnYNIaIa7guaF4eLt4y31wGplpfdJS5gQ8Emrv5dISFvyXscpOB.Q+eyxuhQvXDgW+e+e+s5LBlwsE7e96yyITJ8ac44TNgvGUeqsNnomE3aBbX9z3v7yFNLkvf3AE5Bcj5SfjCUvcZCkGrwPTvCppw8p4XU+Di0YiYlTaL2KUy.MHb1HlFwP.ioQLS4Psp.dypN93CwSKMtLeJrciHXCwDsK7p5s7gtjvmLJPkjV8yUL41BO4Vpeg0wX9aXwAkeCebGpeezmhgJRr7XiK3AR+9Y8ARGLyOP5d1gfIbfukGbcs.rg7LOAOSYdMvgQdoEWPJkTL2aKv8jj6l0iIZJSDNeM0jAiSMS6Rjpq+5GHRTZiAuwYu.avYYXm7dkVQvcR4uZhgrhIjMkIO4NqYrpS5yEjj+mcOR76uyBme1L2K4crWH1FaS5OvE2z6XrKbKKtM9qgqU0wJxMLlZ5bpcodzA8ndDa4MX6yJ82sKN0lno5PqGFZwZAKlxsquO1EaEHkm86q+4PGFV96x9Cdb0vBiYGKtn30mnJLWDqP.5WF8vL+uf5g4cQFJTq7m.Q52GGw99XM5aY6Seps3EgXod2jSA7aO9eUwET2kMFM9cjTU0KpqzGJf+Taa1tiB.9LccLuB5T5JnS4qfNUtB5r5UPmpWAcV6B0gc145Qgz9h8+.gVMEu.QFoFrU9AjroNXE

clumsybear

@orange said in event.drag has a "dead zone":

you can use logaritmic or other non-linear equations for this kind of implementations. Here is my method, I used a "Hyperbolic Decline Equation" method for the frequency cordinates.

I have a question regarding the non-linear equation. As I understand, the non-linear equation is using the knob values as coordinates to map them to the logarithmic frequency response of the Curve EQ. So, if the user is trying to automate the knobs, the values would not correspond to the actual frequencies in Hz, right?

How can we show the actual frequencies, not the linear coordinates?

orange

@clumsybear Yeah the real values won't show up in DAW's automation track, but on the plugin GUI, you can show the corresponding value in a Label (with using the same equation)

DanH

@ustk Would love to know how you made this GraphEQ!

event.drag has a "dead zone"

14

1.8k

10.4k

90.9k